The parallel sides of a trapezium are a and b respectively.

(b) $\frac{1}{2}(a+b)$

Explanation:

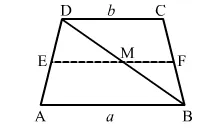
Suppose ABCD is a trapezium.
Draw EF parallel to AB.
Join BD to cut EF at M.
Now, in ∆ DAB, E is the midpoint of AD and EM || AB.

$\therefore M$ is the mid point of $\mathrm{BD}$ and $\mathrm{EM}=\frac{1}{2}(a)$

Similarly, M is the mid point of BD and MF || DC.

i.e., $F$ is the midpoint of $\mathrm{BC}$ and $\mathrm{MF}=\frac{1}{2}(b)$

$\therefore E F=E M+M F=\frac{1}{2}(a+b)$