Question:
The quadrilateral formed by joining the midpoints of the sides of a quadrilateral ABCD, taken in order, is a rhombus, if
(a) ABCD is a Parallelogram
(b) ABCD is rhombus
(c) diagonals of ABCD are equal
(4) diagonals of ABCD are perpendicular to each other.
Solution:
Given:
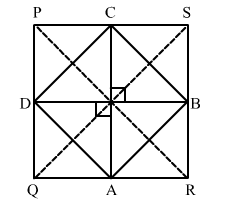
The quadrilateral ABCD is a rhombus.
So, the sides AB, BC, CD and AD are equal.
Now, in $\triangle P Q S$, we have
$D C=\frac{1}{2} Q S$ (Using mid-point theorem) ...(1)
Similarly, in $\triangle P S R$,
$B C=\frac{1}{2} P R$ ..(2)
As, BC = DC
$\Rightarrow \frac{1}{2} Q S=\frac{1}{2} P R$ [From (1) and (2)]
So, QS = PR
Thus, the diagonals of PQRS are equal.
Hence, the correct option is (c).
