The radius of a circle is 13 cm and the length of one of its chords is 10 cm.

(b) 12 cm
Let AB be the chord of the given circle with centre O and a radius of 13 cm.
Then, AB = 10 cm and OB = 13 cm

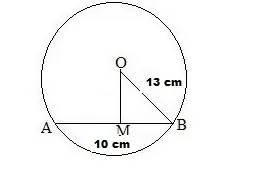
From O, draw OM perpendicular to AB.
We know that the perpendicular from the centre of a circle to a chord bisects the chord.

$\therefore B M=\left(\frac{10}{2}\right) \mathrm{cm}=5 \mathrm{~cm}$

From the right ΔOMB, we have:

$\mathrm{OB}^{2}=\mathrm{OM}^{2}+\mathrm{MB}^{2}$

$\Rightarrow 13^{2}=\mathrm{OM}^{2}+5^{2}$

$\Rightarrow 169=\mathrm{OM}^{2}+25$

$\Rightarrow \mathrm{OM}^{2}=(169-25)=144$

$\Rightarrow \mathrm{OM}=\sqrt{144} \mathrm{~cm}=12 \mathrm{~cm}$

Hence, the distance of the chord from the centre is 12 cm.