The radius of a circle is 20 cm.

The circle can be divided into four parts of equal area by drawing three concentric circles inside it as,

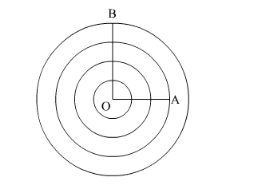
It is given that OB = 20 cm. Let OA = x.

Since the circle is divided into four parts of equal area by the three concentric circles, we have,

Area of the fourth region $=\frac{1}{4} \times$ Area of the given circle

$\pi \times\left(20^{2}-x^{2}\right)=\frac{1}{4} \times \pi \times 20^{2}$

$400-x^{2}=100$

$x^{2}=300$

$x=10 \sqrt{3} \mathrm{~cm}$

Therefore, the correct answer is (b).