The radius of a circle with centre O is 5 cm (Fig . 15.84).

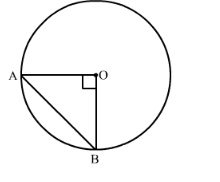
We have given that the radius of the circle is 5 cm.

First we will find the area of the minor segment AB as given below,

Area of the minor segment $\mathrm{AB}=\left(\frac{\pi \theta}{360}-\sin \frac{\theta}{2} \cos \frac{\theta}{2}\right) r^{2}$

Substituting the values we get,

Area of the minor segment $\mathrm{AB}=\left(\frac{3.14 \times 90}{360}-\sin 45 \cos 45\right) 5^{2}$

$\therefore$ Area of the minor segment $\mathrm{AB}=\left(\frac{282.6}{360}-\frac{1}{\sqrt{2}} \times \frac{1}{\sqrt{2}}\right) \times 25$

$\therefore$ Area of the minor segment $A B=\left(\frac{282.6}{360}-\frac{1}{2}\right) \times 25$

$\therefore$ Area of the minor segment $\mathrm{AB}=\left(\frac{565.5-360}{720}\right) \times 25$

$\therefore$ Area of the minor segment $\mathrm{AB}=\frac{205.2}{720} \times 25$

$\therefore$ Area of the minor segment $\mathrm{AB}=\frac{5130}{720}$

$\therefore$ Area of the minor segment $A B=7.125$

Now we will calculate the area of the major segment AB as given below,

$\therefore$ Area of the major segment $\mathrm{AB}=$ Area of the circle-Area of the minor segment

$\therefore$ Area of the major segment $A B=$ Area of the circle-Area of the minor segment

$\therefore$ Area of the major segment $A B=3.14 \times 25-7.125$

$\therefore$ Area of the major segment $\mathrm{AB}=78.5-7.125$

$\therefore$ Area of the major segment $\mathrm{AB}=71.375$

Therefore, areas of the minor and major segments are $7.125 \mathrm{~cm}^{2} 771.375 \mathrm{~cm}^{2}$ respectively.