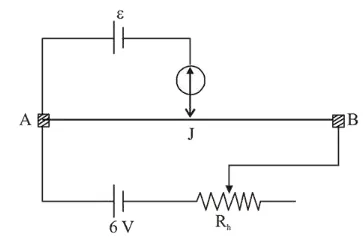
The resistance of the meter bridge $\mathrm{AB}$ in given figure is $4 \Omega$. With a cell of emf $\varepsilon=0.5 \mathrm{~V}$ and rheostat resistance $\mathrm{R}_{\mathrm{h}}=$ $2 \Omega$ the null point is obtained at some point $\mathrm{J}$. When the cell is replaced by another one of $\mathrm{emf} \varepsilon=\varepsilon_{2}$ the same null point $\mathrm{J}$ is found for $\mathrm{R}_{\mathrm{h}}=6 \Omega$. The emf $\varepsilon_{2}$ is,
Correct Option: , 2
(2) Given, Emf of cell, $\varepsilon=0.5 \mathrm{v}$
Rheostat resistance, $\mathrm{R}_{\mathrm{h}}=2 \Omega$
Potential gradient is
$\frac{\mathrm{dv}}{\mathrm{dL}}=\left(\frac{6}{2+4}\right) \times \frac{4}{\mathrm{~L}}$
Let null point be at $\ell \mathrm{cm}$ when cell of emf
$\varepsilon=0.5 \mathrm{v}$ is used.
thus $\varepsilon_{1}=0.5 \mathrm{~V}=\left(\frac{6}{2+4}\right) \times \frac{4}{\mathrm{~L}} \times \ell$ ...(1)
For resistance $R_{h}=6 \Omega$ new potential gradient is
$\left(\frac{6}{4+6}\right) \times \frac{4}{L}$ and at null point
$\left(\frac{6}{4+6}\right)\left(\frac{4}{L}\right) \times \ell=\varepsilon_{2}$ ....(2)
Dividing equation (i) by (ii) we get
$\frac{0.5}{\varepsilon_{2}}=\frac{10}{6}$ thus $\varepsilon_{2}=0.3$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.