The set of all real values

If exactly one root in $(0,1)$ then

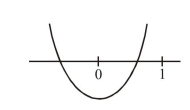
$\begin{array}{ll}\Rightarrow & \mathrm{f}(0) \cdot \mathrm{f}(1)<0 \\ \Rightarrow & 2\left(\lambda^{2}-4 \lambda+3\right)<0 \\ \Rightarrow & 1<\lambda<3\end{array}$

Now for

$\lambda=1,2 \mathrm{x}^{2}-4 \mathrm{x}+2=0$

$(x-1)^{2}=0, x=1,1$

So both roots doesn't lie between $(0,1)$

$\therefore \lambda \neq 1$

Again for $\lambda=3$

$10 x^{2}-12 x+2=0$

$\Rightarrow \quad x=1, \frac{1}{5}$

so if one root is 1 then second root lie between $(0,1)$ so $\lambda=3$ is correct.

$\therefore \quad \lambda \in(1,3] .$