The solubility product of $\mathrm{PbI}_{2}$ is $8.0 \times 10^{-9}$. The solubility of lead iodide in $0.1$ molar solution of lead nitrate is $x \times 10^{-6} \mathrm{~mol} / \mathrm{L}$. The value of $x$ is . (Rounded off to the nearest integer) $[$ Given $: \sqrt{2}=1.41]$
Given : $\left[\mathrm{K}_{\mathrm{sp}}\right]_{\mathrm{PbI}_{2}}=8 \times 10^{-9}$
To calculate : solubility of $\mathrm{PbI}_{2}$ in $0.1 \mathrm{M}$ sol of $\mathrm{Pb}\left(\mathrm{NO}_{3}\right)_{2}$
(I) $\mathrm{Pb}\left(\mathrm{NO}_{3}\right)_{2} \rightarrow \mathrm{Pb}_{\text {(aq) }}^{+2}+2 \mathrm{NO}_{3}^{-}$(aq)
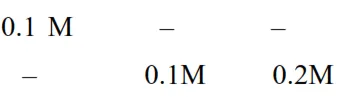
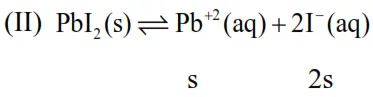
$=\mathrm{s}+0.1$
$\simeq 0.1$
Now : $\mathrm{K}_{\mathrm{sp}}=8 \times 10^{-9}=\left[\mathrm{Pb}^{+2}\right]\left[\mathrm{I}^{-}\right]^{2}$
$\Rightarrow 8 \times 10^{-9}=0.1 \times(2 \mathrm{~s})^{2}$
$\Rightarrow 8 \times 10^{-8}=4 \mathrm{~s}^{2} \Rightarrow \mathrm{s}=\sqrt{2} \times 10^{-4}$
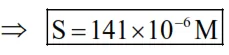
$\Rightarrow x=141$
