Question:
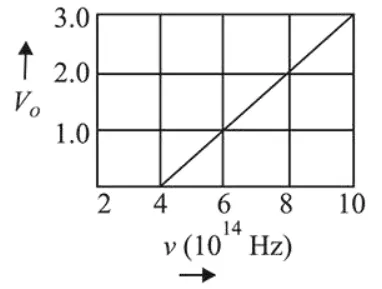
The stopping potential $V_{0}$ (in volt) as a function of frequency $(v)$ for a sodium emitter, is shown in the figure. The work function of sodium, from the data plotted in the figure, will be :
(Given : Planck's constant $(h)=6.63 \times 10^{-34} \mathrm{Js}$, electron charge $e=1.6 \times 10^{-19} \mathrm{C}$ )
Correct Option: , 2
Solution:
(2) $f_{0}=4 \times 10^{14} \mathrm{~Hz}$
$W_{0}=h f_{0}=6.63 \times 10^{-34} \times\left(4 \times 10^{14}\right) \mathrm{J}$
$=\frac{\left(6.63 \times 10^{-34}\right) \times\left(4 \times 10^{14}\right)}{1.6 \times 10^{-19}}$
$=1.66 \mathrm{eV}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.