The sum of squares of two consecutive odd positive integers is 394.

Solution:

Let two consecutive odd positive integer be $(2 x-1)$ and other $(2 x+1)$

Then according to question

$(2 x+1)^{2}+(2 x-1)^{2}=394$

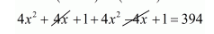
$8 x^{2}+2=394$

$8 x^{2}=394-2$

$x^{2}=\frac{392}{8}$

$x^{2}=49$

$x=\sqrt{49}$

$=\pm 7$

Since, x being a positive number, so x cannot be negative.

Therefore,

When $x=7$ then odd positive

$2 x-1=2 \times 7-1$

$=13$

And

$2 x+1=2 \times 7+1$

$=15$

Thus, two consecutive odd positive integer be 13,15