Question:
The sum of the squares of the lengths of the chords intercepted on the circle, $x^{2}+y^{2}=16$, by the lines, $x+y=\mathrm{n}$, $n \in N$, where $N$ is the set of all natural numbers, is :
Correct Option: , 4
Solution:
Let the chord $x+y=n$ cuts the circle $x^{2}+y^{2}=16$ at $P$ and $Q$ Length of perpendicular from $\mathrm{O}$ on $P Q$
$=\left|\frac{0+0-n}{\sqrt{1^{2}+1^{2}}}\right|=\frac{n}{\sqrt{2}}$
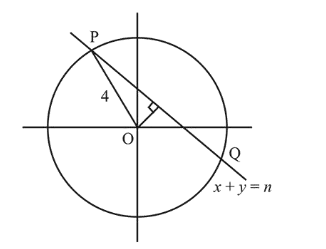
Then, length of chord $P Q=2 \sqrt{4^{2}-\left(\frac{n}{\sqrt{2}}\right)^{2}}$
$=2 \sqrt{16-\frac{n^{2}}{2}}$
Thus only possible values of $n$ are $1,2,3,4,5$.
Hence, the sum of squares of lengths of chords
$=\sum_{n=1}^{5} 4\left(16-\frac{n^{2}}{2}\right)$
$=64 \times 5-2 \cdot \frac{5 \times 6 \times 11}{6}=210$
