Question:
The sum of two forces $\vec{P}$ and $\vec{Q}$ is $\vec{R}$ such that $|\vec{R}|=|\vec{P}|$. The angle $\theta$ (in degrees) that the resultant of 2 $\vec{P}$ and $\vec{Q}$ will make with $\vec{Q}$ is__________
Solution:
(90) Given,
$|\vec{R}|=|\vec{P}| \Rightarrow|\vec{P}+\vec{Q}|=|\vec{P}|$
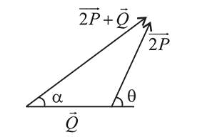
$P^{2}+Q^{2}+2 P Q \cdot \cos \theta=P^{2}$
$\Rightarrow Q+2 P \cos \theta=0$
$\Rightarrow \cos \theta=-\frac{Q}{2 P}$ ...(i)
$\tan \alpha=\frac{2 P \sin \theta}{Q+2 P \cos \theta}=\infty(\because 2 \mathrm{P} \cos \theta+Q=0)$
$\Rightarrow \alpha=90^{\circ}$
