The sum of two number a and b is 15,

Given that $a$ and $b$ be two numbers in such a way that $b=(15-a)$.

Then according to question

$\frac{1}{a}+\frac{1}{b}=\frac{3}{10}$

$\frac{(b+a)}{a b}=\frac{3}{10}$

$\frac{(a+b)}{a b}=\frac{3}{10}$

By cross multiplication

$10 a+10 b=3 a b$....(1)

Now putting the value of b in equation (1)

$10 a+10(15-a)=3 a(15-a)$

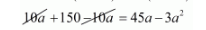
$3 a^{2}-45 a+150=0$

$3\left(a^{2}-15 a+50\right)=0$

$\left(a^{2}-15 a+50\right)=0$

$a^{2}-10 a-5 a+50=0$

$a(a-10)-5(a-10)=0$

$(a-10)(a-5)=0$

$(a-10)=0$

$a=10$

Or

$(a-5)=0$

$a=5$

Therefore,

When $a=10$ then;

$b=15-a=15-10$

$=5$

And when $a=5$ then

$b=15-a=15-5$

$=10$

Thus, two consecutive number be either $a=5, b=10$ or $a=10, b=5$