The table given below shows the marks obtained by 30 students in a test.
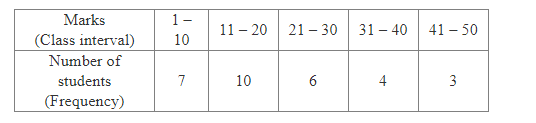
Out of these students, one is chosen at random. What is the probability that the marks of the chosen student
(i) are 30 or less?
(ii) are 31 or more?
(iii) lie in the interval 21 – 30?
Total number of students = 30
(i) Number of students whose marks are 30 or less = 7 + 10 + 6 = 23
$\therefore P$ (Marks of the chosen student are 30 or less) $=\frac{\text { Number of students whose marks are } 30 \text { or less }}{\text { Total number of students }}=\frac{23}{30}$
(ii) Number of students whose marks are 31 or more = 4 + 3 = 7
$\therefore P$ (Marks of the chosen student are 31 or more) $=\frac{\text { Number of students whose marks are } 31 \text { or more }}{\text { Total number of students }}=\frac{7}{30}$
(iii) Number of students whose marks lie in the interval 21–30 = 6
$\therefore P($ Marks of the chosen student lie in the interval $21-30)=\frac{\text { Number of students whose marks lie in the interval } 21-30}{\text { Total number of students }}=\frac{6}{30}=\frac{1}{5}$
