The tangent and normal to the ellipse $3 x^{2}+5 y^{2}=32$ at the point $\mathrm{P}(2,2)$ meet the $\mathrm{x}$-axis at $\mathrm{Q}$ and $\mathrm{R}$, respectively. Then the area (in sq. units) of the triangle $P Q R$ is :
Correct Option: , 4
$3 x^{2}+5 y^{2}=32 \Rightarrow \frac{3 x^{2}}{32}+\frac{5 y^{2}}{32}=1$
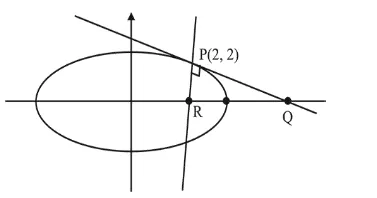
Tangent on the ellipse at $\mathrm{P}$ is
$\frac{3(2) x}{32}+\frac{5(2) y}{32}=1 \Rightarrow \frac{3 x}{16}+\frac{5 y}{16}=1$
$\therefore$ co-ordinates of $Q$ will be $\left(\frac{16}{3}, 0\right)$
Now, normal at $\mathrm{P}$ is $\frac{32}{3(2)}-\frac{32 y}{5(2)}=\frac{32}{3}-\frac{32}{5}$
$\therefore$ co-ordinates of $\mathrm{R}$ will be $\left(\frac{4}{5}, 0\right)$
Hence, area of $\triangle \mathrm{PQR~}=\frac{1}{2}(P Q)(P R)$
$=\frac{1}{2} \sqrt{\frac{136}{9}} \sqrt{\frac{136}{25}}=\frac{68}{15}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.