The tangent to the circumcircle of an isosceles

Solution:

True
Let EAF be tangent to the circumcircle of ΔABC.

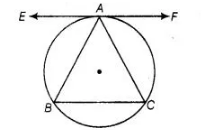
To prove $F A F \| B C$

$\angle E A B=\angle A B C$

Here. $A B=A C$

$\Rightarrow$ $\angle A B C=\angle A C B$$\ldots(1)$

[angle between tangent anc is chord equal to angle made by chord in the alternate segment]

$\therefore$ Also, $\quad \angle E A B=\angle B C A$ ....(ii)

From Eqs. (i) and (ii), we get

$\angle E A B=\angle A B C$

$\Rightarrow \quad E A F \| B C$