The time taken by a person to cover 150 km was 2.5 hrs more than the time taken in the return journey.

Let the ongoing speed of person be $x \mathrm{~km} / \mathrm{hr}$. Then,

Returning speed of the person is $=(x+10) \mathrm{km} / \mathrm{hr}$.

Time taken by the person in going direction to cover $150 \mathrm{~km}=\frac{150}{x} \mathrm{hr}$

Time taken by the person in returning direction to cover $150 \mathrm{~km}=\frac{150}{(x+10)} \mathrm{hr}$

Therefore,

$\frac{150}{x}-\frac{150}{(x+10)}=\frac{5}{2}$

$\frac{\{150(x+10)-150 x\}}{x(x+10)}=\frac{5}{2}$

$\frac{150 x+1500-150 x}{x^{2}+10 x}=\frac{5}{2}$

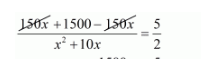
$\frac{1500}{x^{2}+10 x}=\frac{5}{2}$

$3000=5 x^{2}+50 x$

$5 x^{2}+50 x-3000=0$

$5 x^{2}+50 x-3000=0$

$5\left(x^{2}+10 x-600\right)=0$

$x^{2}+10 x-600=0$

$x^{2}-20 x+30 x-600=0$

$x(x-20)+30(x-20)=0$

$(x-20)(x+30)=0$

So, either 

$(x-20)=0$

$x=20$

Or

$(x+30)=0$

$x=-30$

But, the speed of the train can never be negative.

Thus, when $x=20$ then

$=(x+10)$

$=(20+10)$

$=30$

Hence, ongoing speed of person is $x=20 \mathrm{~km} / \mathrm{hr}$

and returning speed of the person is $x=30 \mathrm{~km} / \mathrm{hr}$ respectively.