Question:
The total number of two digit numbers 'n', such that $3^{n}+7^{n}$ is a multiple of 10 , is
Solution:
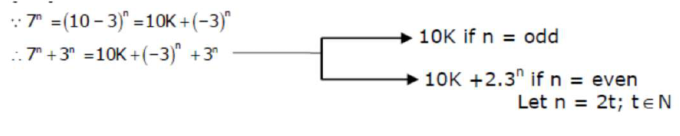
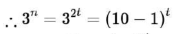
$=10 p+(-1)^{t}$
$=10 p \pm 1$
$\therefore$ if $\mathrm{n}=$ even then $7^{n}+3^{n}$ will not be multiply of 10
So if $n$ is odd then only $7^{n}+3^{n}$ will be multiply of 10
$\therefore \mathrm{n}=11,13,15, \ldots \ldots, \ldots, 99$
$\therefore$ Ans 45
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.