Question:
The value of acceleration due to gravity is $g_{1}$ at a height
$h=\frac{R}{2}(R=$ radius of the earth $)$ from the surface of the earth. It is again equal to $g_{1}$ and a depth $d$ below the surface
of the earth. The ratio $\left(\frac{d}{R}\right)$ equals :
Correct Option: , 2
Solution:
(2) According to question, $g_{h}=g_{d}=g_{1}$
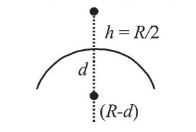
$g_{h}=\frac{G M}{\left(R+\frac{R}{2}\right)^{2}}$ and $g_{d}=\frac{G M(R-d)}{R^{3}}$
$\frac{G M}{\left(\frac{3 R}{2}\right)^{2}}=\frac{G M(R-d)}{R^{3}} \Rightarrow \frac{4}{9}=\frac{(R-d)}{R}$
$\Rightarrow 4 R=9 R-9 d \Rightarrow 5 R=9 d$
$\therefore \frac{d}{R}=\frac{5}{9}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.