The vertex A of ∆ABC is joined to a point D on the side BC.

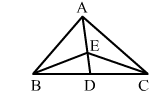
Given:  D is the midpoint of BC and E is the midpoint of AD.

To prove: $\operatorname{ar}(\Delta B E C)=\frac{1}{2} \operatorname{ar}(\Delta A B C)$

Proof: 
Since E is the midpoint of AD, BE is the median of ∆ABD.
We know that a median of a triangle divides it into two triangles of equal areas.

i.e., $\operatorname{ar}(\Delta B E D)=\frac{1}{2} \operatorname{ar}(\Delta A B D)$             .....(i)

Also, $\operatorname{ar}(\Delta C D E)=\frac{1}{2} \operatorname{ar}(\Delta A D C)$         .........(ii)

From (i) and (ii), we have:

$\operatorname{ar}(\Delta B E D)+\operatorname{ar}(\Delta C D E)=\frac{1}{2} \times \operatorname{ar}(\Delta A B D)+\frac{1}{2} \times \operatorname{ar}(\Delta A D C)$

$\Rightarrow \operatorname{ar}(\Delta B E C)=\frac{1}{2} \times[\operatorname{ar}(\Delta A B D)+\operatorname{ar}(\Delta A D C)]$

$\Rightarrow \operatorname{ar}(\Delta B E C)=\frac{1}{2} \times \operatorname{ar}(\Delta A B C)$