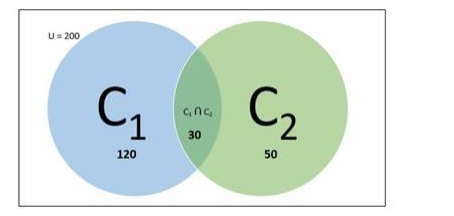
There are 200 individuals with a skin disorder,

Given:

Total number of individuals with skin disorder $=200$

Individuals exposed to chemical $C_{1}=120$

Individuals exposed to chemical $C_{2}=50$

Individuals exposed to chemicals $C_{1}$ and $C_{2}$ both $=30$

To Find:

(i) Individuals exposed to Chemical $C_{1}$ but not $C_{2}$

Let us consider,

Total number of individuals with skin disorder = n(C) = 200

Individuals exposed to chemical $C_{1}=n\left(C_{1}\right)=120$

Individuals exposed to chemical $\mathrm{C}_{2}=\mathrm{n}\left(\mathrm{C}_{2}\right)=50$

Individuals exposed to chemicals $C_{1}$ and $C_{2}$ both $=n\left(C_{1} \cap C_{2}\right)=30$

Individuals exposed to Chemical $C_{1}$ but not $C_{2}=n\left(C_{1}-C_{2}\right)$

Venn diagram:

Now

$n\left(C_{1}-C_{2}\right)=n\left(C_{1}\right)-n\left(C_{1} \cap C_{2}\right)$

$=120-30$

$=90$

Therefore, number of individuals exposed to chemical $C_{1}$ but not $C_{2}=90$

(ii) Individuals exposed to Chemical $C_{2}$ but not $C_{1}$

Let us consider number of Individuals exposed to Chemical $C_{2}$ but not $C_{1}=n\left(C_{2}-C_{1}\right)$

Now,

$\mathrm{n}\left(\mathrm{C}_{2}-\mathrm{C}_{1}\right)=\mathrm{n}\left(\mathrm{C}_{2}\right)-\mathrm{n}\left(\mathrm{C}_{1} \cap \mathrm{C}_{2}\right)$

$=50-30$

$=20$

Therefore, number of individuals exposed to chemical $C_{2}$ but not $C_{1}=20$

(iii) Individuals exposed to Chemical $C_{1}$ or chemical $C_{2}$

Let us consider number of Individuals exposed to Chemical $C_{1}$ or chemical $C_{2}=$ $n\left(C_{1} \cup C_{2}\right)$

Now,

$n\left(C_{1} \cup C_{2}\right)=n\left(C_{1}\right)+n\left(C_{2}\right)-n\left(C_{1} \cap C_{2}\right)$

$=120+50-30$

$=140$

Therefore, number of individuals exposed to chemical $\mathrm{C}_{1}$ or $\mathrm{C}_{2}=140$