There are three urns containing 2 white and 3 black balls,

Given, we have 3 urns:

Urn 1 = 2 white and 3 black balls

Urn 2 = 3 white and 2 black balls

Urn 3 = 4 white and 1 black balls

Now, the probabilities of choosing either of the urns are

P(U1) = P(U2) = P(U3) = 1/3

Let H be the event of drawing white ball from the chosen urn.

So,

P(H/U1) = 2/5, P(H/U2) = 3/5 and P(H/U3) = 4/5

By using Baye’s Theorem, we have

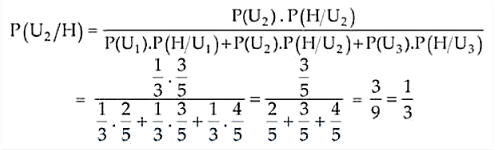
Therefore, the required probability is 1/3.