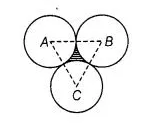
Three circles each of radius 3.5 cm

Given that, three circles are in such a way that each of them touches the other two.

Now, we join centre of all three circles to each other by a line segment. Since, radius of each circle is 3.5 cm.

So;                                             AB = 2 x Radius of circle

= 2 x 3.5 = 7 cm.

⇒                                               AC = BC = AB = 7cm

which shows that, ΔABC is an equilateral triangle with side 7 cm.

We know that, each angle between two adjacent sides of an equilateral triangle is 60°

∴  Area of sector with angle ∠A = 60°.

$=\frac{\angle \mathrm{A}}{360^{\circ}} \times \pi r^{2}=\frac{60^{\circ}}{360^{\circ}} \times \pi \times(3.5)^{2}$

So, $\quad$ area of each sector $=3 \times$ Area of sector with angle $A$.

$=3 \times \frac{60^{\circ}}{360^{\circ}} \times \pi \times(3.5)^{2}$

$=\frac{1}{2} \times \frac{22}{7} \times 3.5 \times 3.5$

$=11 \times \frac{5}{10} \times \frac{35}{10}=\frac{11}{2} \times \frac{7}{2}$

$=\frac{77}{4}=19.25 \mathrm{~cm}^{2}$

and $\quad$ Area of $\Delta A B C=\frac{\sqrt{3}}{4} \times(7)^{2}$ $\left[\because\right.$ area of an equilateral triangle $\left.=\frac{\sqrt{3}}{4}(\text { side })^{2}\right]$

$=49 \frac{\sqrt{3}}{4} \mathrm{~cm}^{2}$

- Area of shaded region enciosed between these circles $=$ Area of $\triangle A B C$

$=21.2176-1925=1.9676 \mathrm{~cm}^{2}$

Hence, the required area enclosed between these circles is $1.967 \mathrm{~cm}^{2}$ (approx).