Three solid spheres each of mass $m$ and diameter $d$ are stuck together such that the lines connecting the centres form an equilateral triangle of side of length $d$. The ratio $\frac{\mathrm{I}_{0}}{\mathrm{I}_{\mathrm{A}}}$ of moment of inertia $\mathrm{I}_{0}$ of the system about an axis passing the centroid and about center of any of the spheres $\mathrm{I}_{\mathrm{A}}$ and perpendicular to the plane of the triangle is:
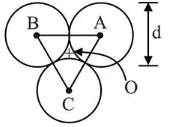
Correct Option: 1
(1) Moment of inertia,
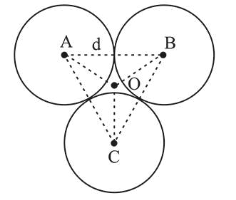
$I_{1}=\frac{2}{5} m\left(\frac{d}{2}\right)^{2}+m(A O)^{2}$
and $A O=\frac{d}{\sqrt{3}}$
Moment of inertia about 'O'
$I_{0}=3 I_{1}=3\left[\frac{2}{5} m\left(\frac{d}{2}\right)^{2}+m\left(\frac{d}{\sqrt{3}}\right)^{2}\right]$
$\Rightarrow I_{0}=\frac{13}{10} \mathrm{Md}^{2}$
And $I_{A}=2\left[\frac{2}{5} M\left(\frac{d}{2}\right)^{2}+M d^{2}\right]+\frac{2}{5} M\left(\frac{d}{2}\right)^{2}$
$\Rightarrow I_{A}=\frac{23}{10} M d^{2}$
$\therefore \frac{I_{O}}{I_{A}}=\frac{\frac{13}{10} M d^{2}}{\frac{23}{10} M d^{2}}=\frac{13}{23}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.