Train A and train B are running on parallel tracks in the opposite directions with speeds of $36 \mathrm{~km} /$ hour and $72 \mathrm{~km} /$ hour, respectively. A person is walking in train $\mathrm{A}$ in the direction opposite to its motion with a speed of $1.8 \mathrm{~km} / \mathrm{hr}$. Speed (in $\mathrm{ms}^{-1}$ ) of this person as observed from train B will be close to : (take the distance between the tracks as negligible)
Correct Option: , 2
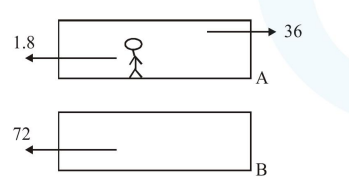
Velocity of man with respect to ground
$\overrightarrow{\mathrm{V}}_{\mathrm{m} / \mathrm{g}}=\overrightarrow{\mathrm{V}}_{\mathrm{m} / \mathrm{A}}+\overrightarrow{\mathrm{V}}_{\mathrm{A}}=-1.8+36$
Velocity of man w.r.t. B
$\overrightarrow{\mathrm{V}}_{\mathrm{m} / \mathrm{B}}=\overrightarrow{\mathrm{V}}_{\mathrm{m}}-\overrightarrow{\mathrm{V}}_{\mathrm{B}}$
$=-1.8+36-(-72)$
$=106.2 \mathrm{~km} / \mathrm{hr}$
$=29.5 \mathrm{~m} / \mathrm{s}$
