Two Carnot engines A and B operate in series such that engine $A$ absorbs heat at $T_{1}$ and rejects heat to a sink at temperature $T$. Engine $B$ absorbs half of the heat rejected by Engine A and rejects heat to the sink at $\mathrm{T}_{3}$. When workdone in both the cases is equal, to value of $T$ is :
Correct Option: , 4
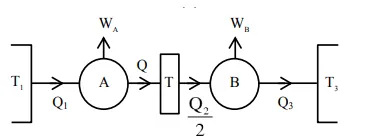
$\mathrm{W}_{\mathrm{A}}=1-\frac{\mathrm{Q}_{2}}{\mathrm{Q}_{1}}=1-\frac{\mathrm{T}}{\mathrm{T}_{1}} \Rightarrow \frac{\mathrm{Q}_{2}}{\mathrm{Q}_{1}}=\frac{\mathrm{T}}{\mathrm{T}_{1}}$
$\mathrm{W}_{\mathrm{B}}=1-\frac{\mathrm{Q}_{3}}{\left(\mathrm{Q}_{2} / 2\right)}=1-\frac{\mathrm{T}_{3}}{\mathrm{~T}} \Rightarrow \frac{2 \mathrm{Q}_{3}}{\mathrm{Q}_{2}}=\frac{\mathrm{T}_{3}}{\mathrm{~T}}$
Now, $\mathrm{W}_{\mathrm{A}}=\mathrm{W}_{\mathrm{B}}$
$\mathrm{Q}_{1}-\mathrm{Q}_{2}=\frac{\mathrm{Q}_{2}}{2}-\mathrm{Q}_{3}$
$\Rightarrow \frac{2 Q_{1}}{Q_{2}}+\frac{2 Q_{3}}{Q_{2}}=3$
$\Rightarrow \frac{2 T_{1}}{T}+\frac{T_{3}}{T}=3$
$\frac{2 T_{1}}{3}+\frac{T_{3}}{3}=T$
