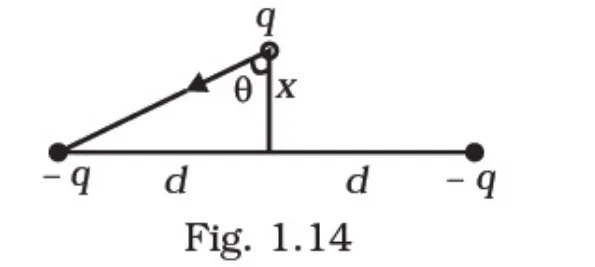
Two charges –q each are fixed separated by distance 2d. A third charge q of mass m placed at the mid-point is displaced slightly by x (x<<d) perpendicular to the line joining the two fixed charged as shown in Fig. 1.14.
Show that q will perform simple harmonic oscillation of time period.
$T=\left[\frac{8 \pi^{3} \varepsilon_{0} m d^{3}}{q^{2}}\right]^{1 / 2}$
Net force F on q towards the centre $\mathrm{O}$
$F=2 \frac{q^{2}}{4 \pi \varepsilon_{\theta} r^{2}} \cos \theta=-\frac{2 q^{2}}{4 \pi \varepsilon_{\theta} r^{2}} \cdot \frac{x}{r}$
$F=-\frac{2 q^{2}}{4 \pi \varepsilon_{0}} \cdot \frac{x}{\left(d^{2}+x^{2}\right)^{1 / 2}}$
$\approx-\frac{2 q^{2}}{4 \pi \varepsilon_{0} d^{3}} x=-k ;$ for $x< Thus, the force on the third charge $q$ is proportional to the displacement and is towards the centre of the two other charges. Therefore, the motion of the third charge is harmonic with frequency $\omega=\sqrt{\frac{K}{m}}$ $\Rightarrow T=\frac{2 \pi}{\omega}=2 \pi \sqrt{\frac{m}{K}}$ $\Rightarrow T=2 \pi \sqrt{\frac{m .4 \pi e_{\nu} d^{3}}{2 q^{2}}}=\left[\frac{8 \pi^{3} \varepsilon_{0} m d^{3}}{q^{2}}\right]^{1 / 2}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.