Question:
Two circles of same radii r and centres O and O' touch each other at P as shown in Fig. 10.91. If O O' is produced to meet the cirele C (O', r) at A and AT is a tangent to the circle C (O,r) such that O'Q
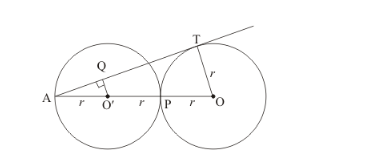
(a) 3/2
(b) 2
(c) 3
(d) 1/4
Solution:
From the given figure we have,
AO = r + r + r
AO = 3r
AO’ = r
Therefore,
$\frac{A O}{A O^{\prime}}=\frac{3 r}{r}$
$\frac{A O}{A O^{\prime}}=3$
Also as $O^{\prime} Q \| O T$ therefore $\frac{A T}{A Q}=\frac{A O}{A O^{\prime}}$
Therefore, option (c) is correct.
