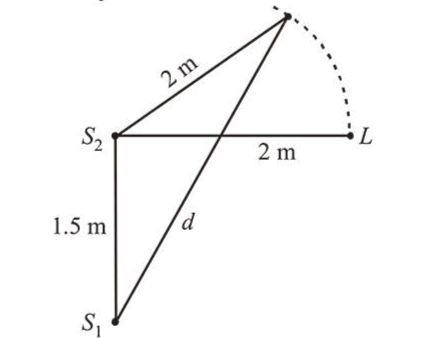
Two coherent sources of sound, $S_{1}$ and $S_{2}$, produce sound waves of the same wavelength, $\lambda=1 \mathrm{~m}$, in phase. $S_{1}$ and $S_{2}$ are placed $1.5 \mathrm{~m}$ apart (see fig.). A listener, located at $L$, directly in front of $S_{2}$ finds that the intensity is at a minimum when he is $2 \mathrm{~m}$ away from $S_{2}$. The listener moves away from $S_{1}$, keeping his distance from $S_{2}$ fixed. The adjacent maximum of intensity is observed when the listener is at a distance $d$ from $S_{1}$. Then, $d$ is :
Correct Option: , 4
(4) Initially, $S_{2} L=2 \mathrm{~m}$
$S_{1} L=\sqrt{2^{2}+\left(\frac{3}{2}\right)^{2}}=\frac{5}{2}=2.5 \mathrm{~m}$
Path difference, $\Delta x=S_{1} L-S_{2} L=0.5 \mathrm{~m}=\frac{\lambda}{2}$
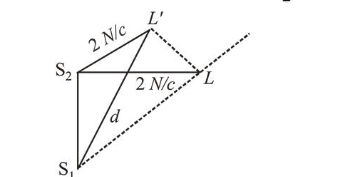
When the listner move from $L$, first maxima will appear if path difference is integral multiple of wavelength.
For example
$\Delta x=n \lambda=1 \lambda \quad \quad(n=1$ for first maxima $)$
$\therefore \Delta x=\lambda=S_{1} L^{\prime}-S_{2} L$
$\Rightarrow 1=d-2 \Rightarrow d=3 \mathrm{~m}$
