Question:
Two concave mirrors of equal radi of curvature $R$ are fixed on a stand facing opposite directions. The whole system has a mass $m$ and is kept on a frictionless horizontal table (fig.)
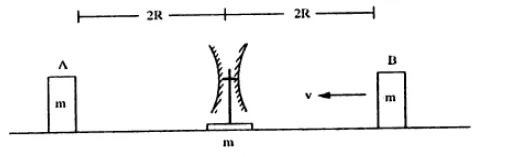
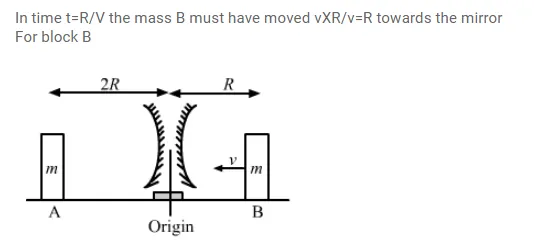
Two block $A$ and $B$ each mass $m$, are placed on the two sides of the stand $A t d=0$, the separation between $\mathrm{A}$ and the mirror is $2 \mathrm{R}$ and also the separation between $\mathrm{B}$ and the mirror is $2 \mathrm{R}$. The block B moves towards the mirror at a speed v. All collisions which takes place are elastic. Taking the original position of the mirror stand system to be $X=0$ and $X$-axis along $A B$, find the position of the images of $A$ and $B$ at $t=$
(a) R/v
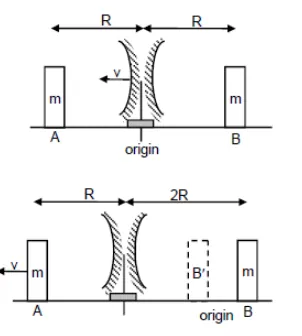
(b) 3R/v
(c) 5R/v
Solution: