Two concentric circles are of radii 5 cm and 3 cm.

Let us first draw whatever is given in the problem so that we can understand the problem better.

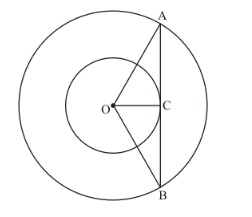
We have to find the length of AB, which is the chord of the larger circle which touches the smaller circle.

Clearly, OC is the radius of the smaller circle and is touching the tangent AB.

We know that the radius of the circle will always form a right angle with the tangent at the point of contact.

We have draw OA in order to complete the triangle OAC which will be a right triangle.

From the figure it is very clear that OA is the radius of the larger circle which is 5 cm.

We can now find AC using Pythagoras theorem. We have,

$\mathrm{AC}^{2}=\mathrm{OA}^{2}-\mathrm{OC}^{2}$

$=5^{2}-3^{2}$

$=25-9$

$=16$

$\mathrm{AC}=\sqrt{16}$

$=4$

Similarly we can find CB. We have,

$\mathrm{CB}^{2}=\mathrm{OB}^{2}-\mathrm{OC}^{2}$

$=5^{2}-3^{2}$

$=25-9$

$=16$

$\mathrm{CB}=\sqrt{16}$

$=4$

From the figure we can see that,

AB = AC + CB

Since we have found the values of AC and CB, let us substitute the values in the above equation. We get,

AB = 4 + 4

AB = 8

Therefore, the length of the chord of the larger circle which touches the smaller circle is 8 cm.