Two concentric circles are of radii 5 cm and 3 cm, respectively.

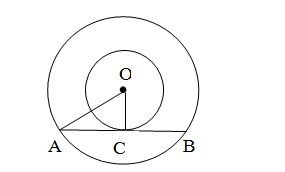
Given: Two circles have the same centre O and AB is a chord of the larger circle touching the
smaller circle at C; also, OA=5 cm and OC=3 cm.  

In $\Delta O A C, O A^{2}=O C^{2}+A C^{2}$

$\therefore A C^{2}=O A^{2}-O C^{2}$

$\Rightarrow A C^{2}=5^{2}-3^{2}$

$\Rightarrow A C^{2}=25-9$

$\Rightarrow A C^{2}=16$

$\Rightarrow A C=4 \mathrm{~cm}$

$\therefore A B=2 A C$ (since perpendicular drawn from the centre of the circle

bisects the chord)

$\therefore A B=2 \times 4=8 \mathrm{~cm}$

The length of the chord of the larger circle is 8 cm.