Two concentric circles of radii 3 cm and 5 cm are given.

Solution:

Consider .

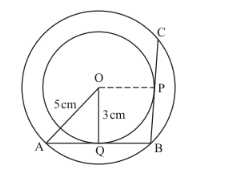
We have,

$\mathrm{OQ} \perp \mathrm{AB}$

Therefore,

$\mathrm{QA}^{2}=\mathrm{OA}^{2}-\mathrm{OQ}^{2}$

$\mathrm{QA}^{2}=5^{2}-3^{2}$

$\mathrm{QA}^{2}=25-9$

 

$\mathrm{QA}^{2}=16$

$\mathrm{QA}=4$

Considering AB as the chord to the bigger circle, as OQ is perpendicular to AB, OQ bisects AB.

∴ AQ = QB = 4 cm.

Now, as BQ and BP are pair of tangents to the inner circle drawn from the external point B, QB = PB = 4 cm.

Now, join OP.

Then, .

⇒ OP bisects BC

⇒ BP = PC = 4 cm

Thus, BC = 4 cm + 4 cm = 8 cm

Therefore, option (c) is correct.