Two dice are tossed once.

Given : two dice are tossed once

To find : Probability of getting an even number on the first die or a total 8.

The formula used : Probability =

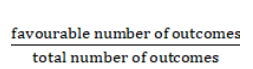
$P(A$ or $B)=P(A)+P(B)-P(A$ and $B)$

A die is numbered from 1 to 6

When two dice are tossed once, total number of outcomes $=6^{2}=36$

Let $A$ denote the event of getting an even number on the first die and $B$ denote the event of getting a total of 8

For getting an even number on the first die

Favourable outcomes =

$\{(2,1),(2,2),(2,3),(2,4),(2,5),(2,6),(4,1),(4,2),(4,3),(4,4),(4,5),(4,6),(6,1),(6,2)$

$,(6,3),(6,4),(6,5),(6,6)\}$

Favourable number of outcomes = 18

Probability of getting an even number on the first die $=P(A)=\frac{18}{36}$

For getting a total of 8

Favourable outcomes =

$\{(2,6),(4,4),(6,2),(5,3),(3,5)\}$

Favourable number of outcomes = 5

Probability of getting a total of $8=P(A)=\frac{5}{36}$

For getting an even number on the first die and a total of 8

Favourable outcomes = {(2,6) , (4,4) , (6,2)}

Probability of getting an even number on the first die and a total of $8=P(A$ and $B)=\frac{3}{36}$

$P(A$ or $B)=P(A)+P(B)-P(A$ and $B)$

$P(A$ or $B)=\frac{18}{36}+\frac{5}{36}-\frac{3}{36}$

$P(A$ or $B)=\frac{18+5-3}{36}=\frac{20}{36}=\frac{5}{9}$

Probability of getting an even number on the first die or a total $8=\frac{5}{9}$