Two equal circles touch each other externally at C and AB is

Let us first put the given data in the form of a diagram.

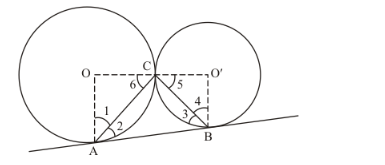
Let us draw radius OA, such that it touches the circle with center O at point A.

Let us draw radius O’B such that it touches the circle with center O’ at point B.

Let us also draw radii from each circle to the point C.

We know that the radius is always perpendicular to the tangent at the point of contact. Therefore,

$\angle O A B=90^{\circ}$

That is,

$\angle 1+\angle 2=90^{\circ}$

$\angle 2=90^{\circ}-\angle 1 \ldots \ldots(1)$

Similarly,

$\angle O^{\prime} B A=90^{\circ}$

$\angle 3+\angle 4=90^{\circ}$.......(2)

$\angle 4=90^{\circ}-\angle 3$

Now, in $\triangle A O C$,

OA = OC(Radii of the same circle)

Therefore,

$\angle 1=\angle 6$ (Angles opposite to equal sides will be equal) ...... (3)

Similarly, in $\Delta C O^{\prime} B$

$\angle 4=\angle 5 .$.....(4)

Consider the straight line OCO’. We have,

$\angle O C O^{\prime}=180^{\circ}$

Looking at the figure, we can rewrite the above equation as,

$\angle 6+\angle A C B+\angle 5=180^{\circ}$

$\angle 2+\angle A C B+\angle 4=180^{\circ}($ From $(3)$ and $(4))$

$\left(90^{\circ}-\angle 1\right)+\angle A C B+\left(90^{\circ}-\angle 3\right)=180^{\circ}$ (From (1) and (2))

$180^{\circ}+\angle A C B-(\angle 1+\angle 3)=180^{\circ}$

$\angle A C B=(\angle 1+\angle 3) \ldots \ldots(5)$

Now let us take up. We have,

$\angle 1+\angle A C B+\angle 3=180^{\circ}$ (Sum of all angles of a triangle will be $180^{\circ}$ )

From equation (5), we get

$\angle A C B+\angle A C B=180^{\circ}$

$2 \angle A C B=180^{\circ}$

$\angle A C B=90^{\circ}$

Therefore the correct answer to this question is choice (d).