Two families with three members each and one family with four members are to be seated in a row. In how many ways can they be seated so that the same family members are not separated ?

Question:
Two families with three members each and one family with four members are to be seated in a row. In how many ways can they be seated so that the same family members are not separated ?

$2 ! 3 ! 4 !$
$(3 !)^{3} \cdot(4 !)$
$(3 !)^{2} \cdot(4 !)$
$3 !(4 !)^{3}$

Correct Option: , 2

Solution:

Total numbers in three familes $=3+3+4=10$ so total arrangement $=10$ !

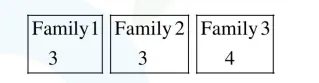
Favourable cases

$=$ $3 !$ $3 ! \times 3 ! \times 4 !$

$\therefore$ Probability of same family memebers are

together $=\frac{3 ! 3 ! 3 ! 4 !}{10 !}=\frac{1}{700}$

so option(2) is correct.

Click here to get exam-ready with eSaral

For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.

All Study Material