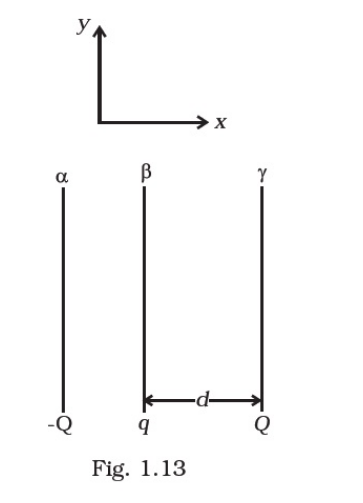
Two fixed, identical conducting plates (α & β), each of surface area S are charged to – Q and q, respectively, where Q > q > 0. A
third identical plate (γ), free to move is located on the other side of the plate with charge q at a distance d (Fig 1.13). The third
plate is released and collides with the plate β. Assume the collision is elastic and the time of collision is sufficient to redistribute
charge amongst β & γ
(a) Find the electric field acting on the plate γ before collision.
(b) Find the charges on β and γ after the collision.
(c) Find the velocity of the plate γ after the collision and at a distance d from the plate β.
There is another useful system of units, besides the SI/mks A system, called the cgs (centimeter-gram-second) system. In this system Coloumb’s law is given by
(a)
Considering right direction to be positive
The electric field at $\gamma$ due to plate $\alpha$ is $-\frac{Q}{S\left(2 \in_{0}\right)}$ [i.e., towards left]
The electric field at $y$ due to plate $\beta$ is $\frac{Q}{S\left(2 \in_{0}\right)}$ [i.e., towards right]
The net electric field $=\frac{q-Q}{S\left(2 \in_{o}\right)}$ [Here, $Q>q$, so direction will be towards left].
(b)
During the collision plates $\beta$ and $\gamma$ are together so they must be at one potential. Charge on $\beta$ is $q_{1}$ and on $\gamma$ is $q_{2}$. Consider a point $\mathrm{O}$. The electric field here must be zero.
Electric field at $O$ due to $\alpha=\frac{-Q}{S\left(2 c_{0}\right)}$, to the left
Electric field at $O$ due to $\beta=\frac{q_{1}}{S\left(2 c_{0}\right)}$, to the right
Electric field at $O$ due $\gamma=\frac{q_{2}}{S\left(2 e_{5}\right)}$ to the left
As the electric field at $O$ is zero, therefore
$\frac{Q+q}{S\left(2 c_{0}\right)}=\frac{q_{1}}{S\left(2 c_{0}\right)}$
$\therefore Q+q_{2}-q_{2} \ldots(1)$
There is no loss of charge on collision, therefore
$Q+q=q_{1}+q_{2} \ldots(i i)$
On solving ...(i) and (ii). we get
$q_{1}=(\rho+q / 2)=$ charge on plates $\beta$
$q_{2}=(q / 2)=$ charge on plate $\gamma$
(c)
Let the velocity be $v$ at the distance $d$ after the collision. If $m$ is the mass of the plate $\gamma$, then the gain in $\mathrm{K}$. E. over the round trip must be equal to the work done by the electric field. After the collision, the electric field at $\gamma$ is
$E_{2}=\frac{-Q}{2 \varepsilon_{0} S}+\frac{(Q+q / 2)}{2 s_{0} S}=\frac{q / 2}{2 c_{0} S}$
The work done when the plate $g$ is released till the collision is $F_{1} d$ where $F_{1}$ is the force on plate $\gamma$.
The work done after the collision till it reaches $d$ is $F_{2} \mathrm{~d}$ is force on plate $\%$.
$F_{1}=E_{1} Q=\frac{(Q-q) Q}{2 \varepsilon_{0} S}$
$F_{2}=E_{2} q / 2=\frac{(q / 2)^{2}}{2 \varepsilon_{0} S}$
Total work done $=\left(F_{1}+F_{2}\right) d=\left[\frac{(Q-q) Q}{2 \varepsilon_{0} S}+\frac{(q / 2)^{2}}{2 \varepsilon_{0} S}\right] d=\frac{(Q-q / 2)^{2} d}{2 \varepsilon_{q} S}$
Using work energy theorem, we have
$\frac{1}{2} m v^{2}=\frac{(Q-q / 2)^{2} d}{2 \varepsilon_{0} S}$
Further solving, we have
$v=(Q-q / 2)\left(\frac{d}{m \varepsilon_{0} S}\right)^{1 / 2}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.