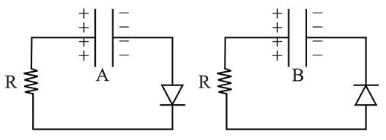
Two identical capacitors $\mathrm{A}$ and $\mathrm{B}$, charged to the same potential 5V are connected in two different circuits as shown below at time $t=0$. If the charge on capacitors $\mathrm{A}$ and $\mathrm{B}$ at time $t=\mathrm{CR}$ is $\mathrm{Q}_{\mathrm{A}}$ and $\mathrm{Q}_{\mathrm{B}}$ respectively, then (Here e is the base of natural logarithm)
Correct Option: , 3
(3) In case I diode is reverse biased, so no current flows
$\therefore \quad Q_{A}=C V$
In case II, current will flow as diode is forward biased. So, it offers negligible resistance to the flow of current and thus be replaced by short circuit. Now, the charge of capacitor will leak through the resistance and decay exponentially with time.
During discharging of capacitor
Potential difference across the capacitor at any instant
$V^{\prime}=V e^{-\frac{t}{C R}}$
But $t=C R$
$V^{\prime}=V e^{-1}=\frac{V}{e}$
$\therefore \quad$ Charge $Q_{B}=C V=\frac{C V}{e}$
