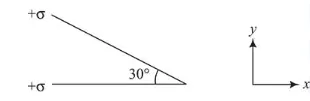
Two infinite planes each with uniform surface charge density

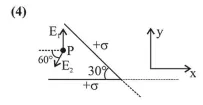
From figure,

$\vec{E}_{1}=\frac{\sigma}{2 \varepsilon_{0}} \hat{y}$ and $\vec{E}_{2}=\frac{\sigma}{2 \varepsilon_{0}}\left(-\cos 60^{\circ} \hat{x}-\sin 60^{\circ} \hat{y}\right)$

$=\frac{\sigma}{2 \varepsilon_{0}}\left(-\frac{1}{2} \hat{x}-\frac{\sqrt{3}}{2} \hat{y}\right)$

Electric field in the region shown in figure $(P)$

$\vec{E}_{P}=\vec{E}_{1}+\vec{E}_{2}=\frac{\sigma}{2 \varepsilon_{0}}\left[-\frac{1}{2} \hat{x}+\left(1-\frac{\sqrt{3}}{2}\right) \hat{y}\right]$

or, $\vec{E}_{P}=\frac{\sigma}{2 \varepsilon_{0}}\left[\left(1-\frac{\sqrt{3}}{2}\right) \hat{y}-\frac{\hat{x}}{2}\right]$