Two lines AB and CD intersect at a point O, such that ∠BOC + ∠AOD = 280°, as shown in the figure.

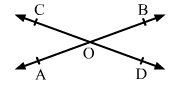
We know that if two lines intersect, then the vertically-opposite angles are equal.

Let $\angle B O C=\angle A O D=x^{\circ}$

Then,

$x+x=280$

$\Rightarrow 2 x=280$

$\Rightarrow x=140^{\circ}$

$\therefore \angle B O C=\angle A O D=140^{\circ}$

Also, let $\angle A O C=\angle B O D=y^{\circ}$

We know that the sum of all angles around a point is $360^{\circ}$.

$\therefore \angle A O C+\angle B O C+\angle B O D+\angle A O D=360^{\circ}$

$\Rightarrow y+140+y+140=360^{\circ}$

$\Rightarrow 2 y=80^{\circ}$

$\Rightarrow y=40^{\circ}$

Hence, $\angle A O C=\angle B O D=40^{\circ}$

$\therefore \angle B O C=\angle A O D=140^{\circ}$ and $\angle A O C=\angle B O D=40^{\circ}$