Two men on either side of the cliff 80 m high observes the angles of a

Solution:

Let AB and AD be the two men either side of cliff and height of cliff is 80 m.

And makes an angle of elevation, 30° and 60° respectively of the top of the cliff

We have given that AC = 80 m. Let BC = x and CD = y. And ,

Here we have to find height of cliff.

We have the corresponding figure as follows

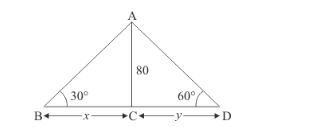
So we use trigonometric ratios.

In a triangle,

$\Rightarrow \quad \tan B=\frac{A C}{B C}$

$\Rightarrow \quad \tan 30^{\circ}=\frac{80}{x}$

$\Rightarrow \quad \frac{1}{\sqrt{3}}=\frac{80}{x}$

$\Rightarrow \quad x=80 \sqrt{3}$

Again in a triangle $A D C$

$\Rightarrow \quad \tan D=\frac{A C}{C D}$

$\Rightarrow \quad \tan 60^{\circ}=\frac{80}{y}$

$\Rightarrow \quad \sqrt{3}=\frac{80}{y}$

$\Rightarrow \quad y=\frac{80}{\sqrt{3}}$

$\Rightarrow \quad x+y=80 \sqrt{3}+\frac{80}{\sqrt{3}}$

$\Rightarrow \quad x+y=\frac{320}{\sqrt{3}}$

$\Rightarrow \quad x+y=184.8$

Hence the height of cliff is $184.8 \mathrm{~m}$.