Two planets have masses $M$ and $16 M$ and their radii are $a$ and $2 a$, respectively. The separation between the centres of the planets is $10 a$. A body of mass $\mathrm{m}$ is fired from the surface of the larger planet towards the smaller planet along the line joining their centres. For the body to be able to reach the surface of smaller planet, the minimum firing speed needed is : respectively. The separation between the centres of the planets is $10 a$. A body of mass $\mathrm{m}$ is fired from the surface of the larger planet towards the smaller planet along the line joining their centres. For the body to be able to reach the surface of smaller planet, the minimum firing speed needed is :
Correct Option: , 4
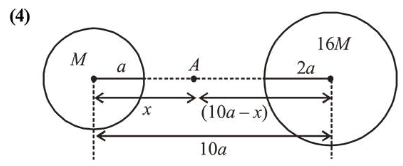
Let $A$ be the point where gravitation field of both planets cancel each other i.e. zero.
$\frac{G M}{x^{2}}=\frac{G(16 M)}{(10 a-x)^{2}}$
$\Rightarrow \frac{1}{x}=\frac{4}{(10 a-x)} \Rightarrow 4 x=10 a-x \Rightarrow x=2 a$ ....(1)
Using conservation of energy, we have
$-\frac{G M m}{8 a}-\frac{G(16 M) m}{2 a}+K E=-\frac{G M m}{2 a}-\frac{G(16 M) m}{8 a}$
$K E=G M m\left[\frac{1}{8 a}+\frac{16}{2 a}-\frac{1}{2 a}-\frac{16}{8 a}\right]$
$\Rightarrow K E=G M m\left[\frac{1+64-4-16}{8 a}\right]$
$\Rightarrow \frac{1}{2} m v^{2}=G M m\left[\frac{45}{8 a}\right] \Rightarrow v=\sqrt{\frac{90 G M}{8 a}}$
$\Rightarrow v=\frac{3}{2} \sqrt{\frac{5 G M}{a}}$
