Two poles of heights 6 m and 11 m stand on a plane ground. If the distance between their feet is 12 m,

Let us draw the diagram from the given information.

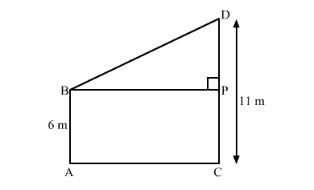
Let us draw a perpendicular from B on CD which meets CD at P.

It is clear that BP = 12 m because it is given that distance between feet of the two poles is 12 m.

After drawing the perpendicular we get a rectangle BACP such that AB = PC and BP = AC.

Because of this construction we also obtained a right angled triangle BPD.

Now we will use Pythagoras theorem,

$B D^{2}=B P^{2}+P D^{2}$

Let us substitute the values of BP and PD we get,

$B D^{2}=12^{2}+5^{2}$

$\therefore B D^{2}=144+25$

$B D^{2}=169$

Taking the square root we get, $B D=13$

Therefore, distance between the top of the two poles is