Two tangent segments PA and PB are drawn to a circle

Let us first put the given data in the form of a diagram. We have,

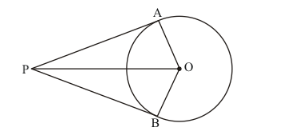
Consider and . We have,

Here, PO is the common side.

PA = PB (Length of two tangents drawn from the same external point will be equal)

OA = OB(Radii of the same circle)

By SSS congruency, we have  is congruent to .

Therefore,

It is given that,

That is,

$\angle A P O+\angle B P O=120^{\circ}$

$2 \angle A P O=120^{-}($Since $\angle A P O=\angle B P O)$

$\angle A P O=60^{\circ}$

In $\triangle P A O$

$\angle P A O=90^{\circ}$ (Since radius will be perpendicular to the tangent at the point of contact)

We know that,

$\cos 60=\frac{A P}{P O}$

$\frac{1}{2}=\frac{A P}{O P}$

$O P=2 A P$

Thus we have proved.