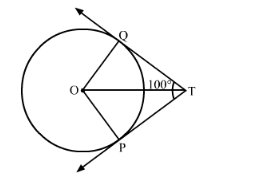
Question:
Two tangents TP and TQ are drawn from an external point T to a circle with centre O as shown in Fig. 10.73. If they are inclined to each other at an angle of 100°, then what is the value of ∠POQ?
Solution:
Consider the quadrilateral OPTQ. It is given that ∠PTQ = 100°.
From the property of the tangent we know that the tangent will always be perpendicular to the radius at the point of contact. Therefore we have,
![]()
![]()
We know that the sum of all angles of a quadrilateral will always be equal to 360°.
Therefore,
![]() +
+ ![]() +
+![]() +
+![]()
Let us substitute the values of all the known angles. We have,
$100^{\circ}+90^{\circ}+90^{\circ}+\angle \mathrm{POQ}=360^{\circ}$
$280+\angle \mathrm{POQ}=360^{\circ}$
$\angle \mathrm{POQ}=80^{\circ}$
Therefore, the value of angle ∠POQ is 80°.
