Two vertical poles of height 9 m and 14 m stand on a plane ground.

Let the two poles be DE and AB and the distance between their bases be BE.
We have:
DE = 9 m, AB = 14 m and BE = 12 m
Draw a line parallel to BE from D, meeting AB at C.
Then, DC = 12 m  and AC = 5 m
We need to find AD, the distance between their tops.

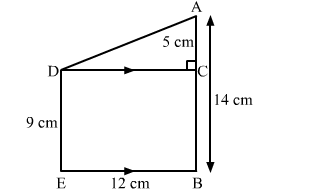
Applying Pythagoras theorem in right-angled triangle ACD, we have: ​

$A D^{2}=A C^{2}+D C^{2}$

$A D^{2}=5^{2}+12^{2}=25+144=169$

$A D=\sqrt{169}=13 \mathrm{~m}$

Hence, the distance between the tops of the two poles is 13 m.