Two vertical poles of heights, $20 \mathrm{~m}$ and $80 \mathrm{~m}$ stand apart on a horizontal plane. The height (in meters) of the point of intersection of the lines joining the top of each pole to the foot of the other, from this horizontal plane is :
Correct Option: , 4
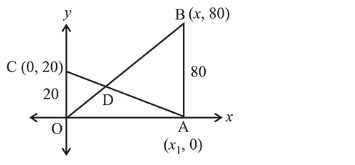
Equations of lines $\mathrm{OB}$ and $\mathrm{AC}$ are respectively
$y=\frac{80}{x_{1}} x$....(i)
$\frac{x}{x_{1}}+\frac{y}{20}=1$..(ii)
$\because$ equations (i) and (ii) intersect each other
$\therefore$ substitute the value of $x$ from equation (i) to equation (ii), we get
$\frac{y}{80}+\frac{y}{20}=1$
$\Rightarrow y+4 y=80 \Rightarrow y=16 \mathrm{~m}$
Hence, height of intersection point is $16 \mathrm{~m}$.
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.