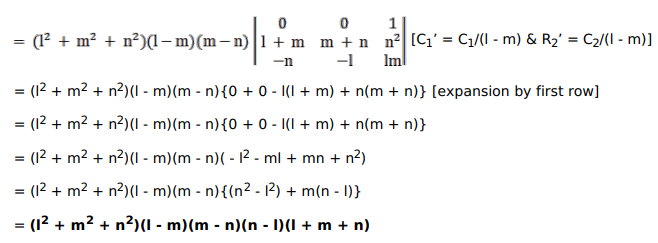Question:
Using properties of determinants prove that:.
$\left|\begin{array}{ccc}(\mathrm{m}+\mathrm{n})^{2} & \mathrm{l}^{2} & \mathrm{mn} \\ (\mathrm{n}+1)^{2} & \mathrm{~m}^{2} & \ln \\ (1+\mathrm{m})^{2} & \mathrm{n}^{2} & \operatorname{lm}\end{array}\right|=\left(\mathrm{l}^{2}+\mathrm{m}^{2}+\mathrm{n}^{2}\right)(1-\mathrm{m})$
$(m-n)(n-1)$
Solution: