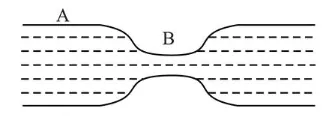
Water flows in a horizontal tube (see figure).

(2) According to question, area of cross-section at $A, a A$ $=40 \mathrm{~cm}^{2}$ and at $B, a B=20 \mathrm{~cm}^{2}$

Let velocity of liquid flow at $A,=V_{A}$ and at $B,=V_{B}$ Using equation of continuity $a_{A} V_{A}=a_{B} V_{B}$

$40 V_{A}=20 V_{B}$

$\Rightarrow \quad 2 V_{A}=V_{B}$

Now, using Bernoulli's equation

$P_{A}+\frac{1}{2} \rho V_{A}^{2}=P_{B}+\frac{1}{2} \rho V_{B}^{2} \Rightarrow P_{A}-P_{B}=\frac{1}{2} \rho\left(V_{B}^{2}-V_{A}^{2}\right)$

$\Rightarrow \Delta P=\frac{1}{2} 1000\left(V_{B}^{2}-\frac{V_{B}^{2}}{4}\right) \Rightarrow \Delta P=500 \times \frac{3 V_{B}^{2}}{4}$

$\Rightarrow V_{B}=\sqrt{\frac{(\Delta P) \times 4}{1500}}=\sqrt{\frac{(700) \times 4}{1500}} \mathrm{~m} / \mathrm{s}=1.37 \times 10^{2} \mathrm{~cm} / \mathrm{s}$

Volume flow rate $\mathrm{Q}=a_{B} \times v_{B}$

$=20 \times 100 \times V_{B}=2732 \mathrm{~cm}^{3} / \mathrm{s} \approx 2720 \mathrm{~cm}^{3} / \mathrm{s}$