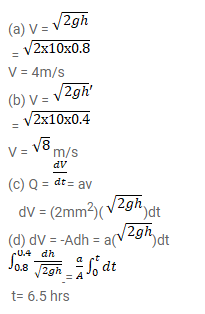Water leaks out from an open tank through a hole of area $2 \mathrm{~mm}^{2}$ in the bottom. Suppose water is filled up to a height of 80 $\mathrm{cm}$ and the area of cross-section of the tank is $0.4 \mathrm{~m}^{2}$. The pressure at the open surface and at the hole are equal to the atmospheric pressure. Neglect the small velocity of the water near the open surface in the tank.
(a) Find the initial speed of water coming out of the hole.
(b) Find the speed of water coming out when half of water has leaked out.
(c) Find the volume of water leaked out during a time internal dt after the height remained is $h$. Thus find the decrease in height dh in terms of $h$ and dt.
(d) From the result of part (c) find the time required for half of the water to leak out.